
The Area of Triangle can be calculated using various formulas including Heron's Formula, and Area of a Triangle Given Two Sides and the Included Angle (SAS) Area of Triangle with Three Sides (Heron’s Formula) Type of Triangleįor a given triangle, where the base of the triangle is b and the height is h, the area of the triangle can be determined by the recipe, such as A = ½ (b × h) sq. The area of triangle formulas for all the different types of triangles like the equilateral triangle, right-angled triangle, and isosceles triangle are given below. However, there are different types of triangles in mathematics that are classified on the basis of their sides and angles. Area of Triangle FormulaĪs defined Area of triangle is ½ × base × height or it can be written as ½ x b x h. There are different types of triangles in mathematics namely Equilateral Triangle, Isosceles Triangle, and Right-Angled Triangle that are classified on the basis of their sides and angles. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180°. Triangle is a 2-D figure and the Mensuration Formula for a triangle is ½ × Base × Height In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. This article will benefit students in studying mathematics, especially geometry. The area of a triangle is expressed in square units, as m², cm², in², and so on. The height is the length between the base and the highest point of the triangle. The base of the triangle is always at the bottom it is the side that the triangle sits on. Basically, it is equal to half of the base times height. The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. The area of a right-angled triangle is defined as the space occupied by the triangle.Area of Triangle: A triangle is a closed figure with 3 angles, 3 sides, and 3 vertices. P (perimeter) = a + b + c (sum of the sides of a triangle) Area of a right-angled triangle The perimeter of a right-angled triangle is defined as the total length of the boundary. Pythagoras discovered that the hypotenuse square equals the sum of the squares of the other two sides in a right-angled triangle.
The Formula for a Right-Angled Triangle Pythagoras theorem In this triangle, all the three sides will be of different lengths, and the three angles will be of different measures. In the scalene right triangle ABC, ∠ A measures 30°, ∠ B measures 90°, and ∠ C measures 60°. Scalene right triangle: This triangle is the one in which one interior angle measures 90°, while the other two have different measures.

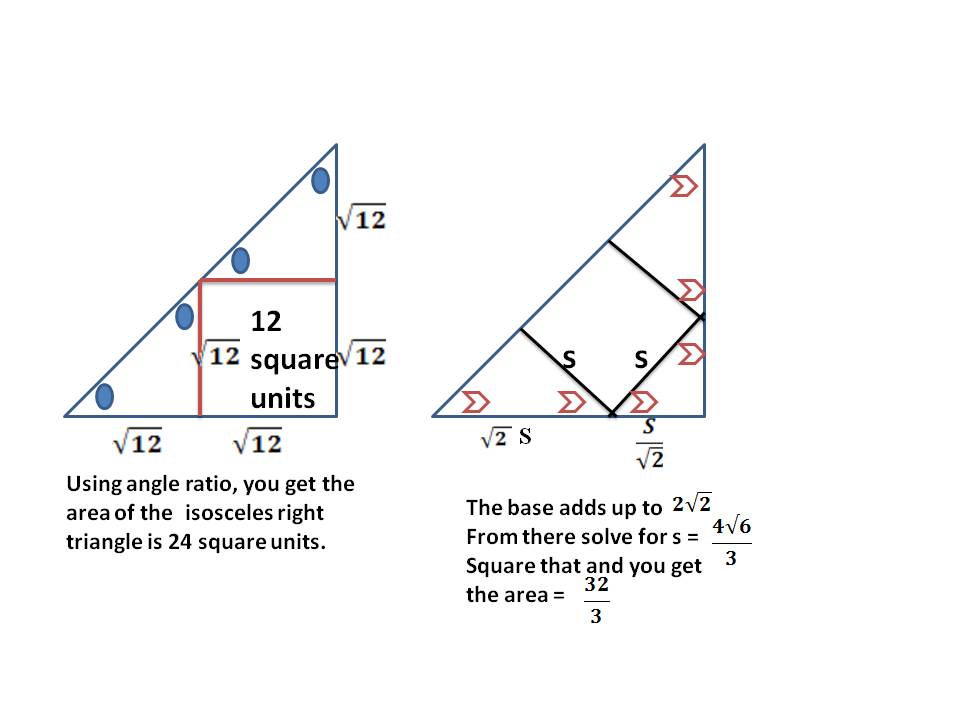
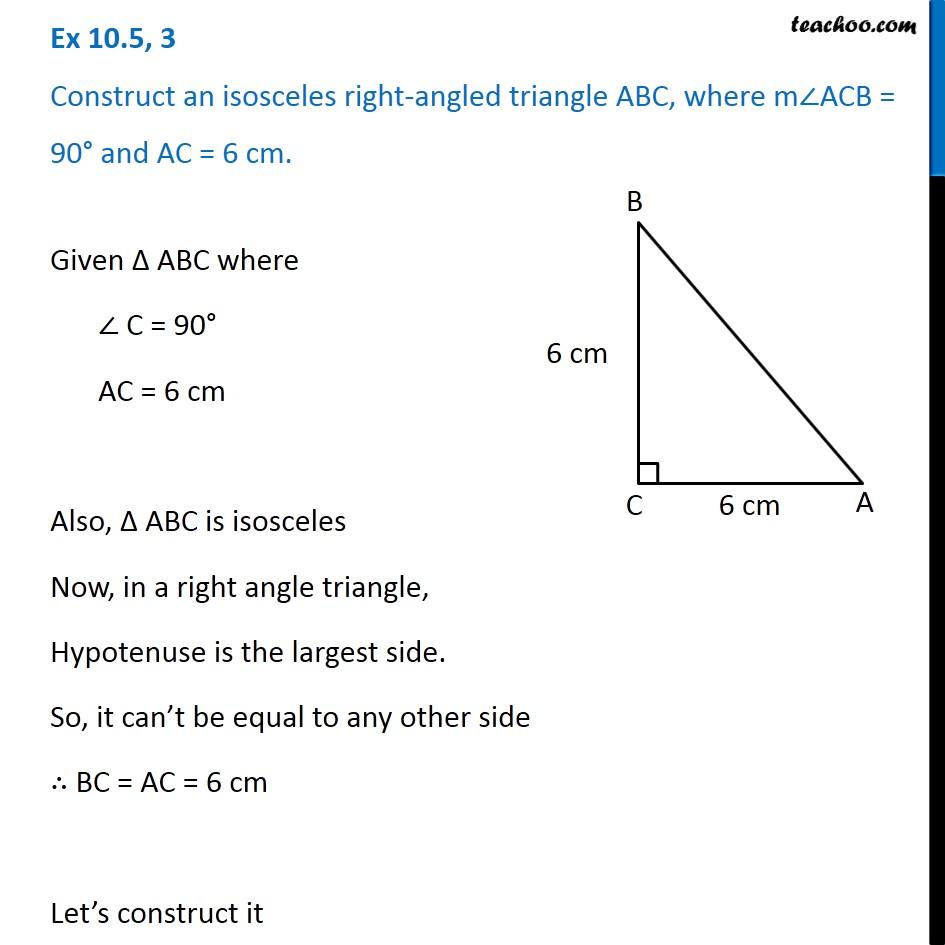
Here, ∠ A and ∠ C measure 45° each because the property states that angles opposite to equal sides are also equal.Ģ. This is an isosceles right triangle, with the sides AB and AC equal and ∠ B measuring 90°. Isosceles right triangle: In this triangle, one interior angle measures 90°, and the other two angles measure 45° each.

The units m 2, cm 2, in 2, yd 2, and others commonly represent the area. The total space or territory covered by a right-angled triangle is known as the area of a right triangle. The longest side of the right triangle, which is also the side opposite the right angle, is the hypotenuse and the two arms of the right angle are the height and the base. A triangle in which one of the interior angles is 90° is called a right triangle.


 0 kommentar(er)
0 kommentar(er)
